We hear the size of the difference in pitch between C' (middle C) and
C'' as the same as the difference between C'' and C'''. We call this difference
"one octave" (made of 12 semitones) in both cases. Yet, the frequency
difference between C' and C'', as measured in Hertz, is not the same as
the frequency difference between C'' and C''', as the following
table and figure
1 show:
| Note | No. of semitones above C' | Multiplier of C' frequency | F (Hz) | log10 F |
| C''' | 24 | 4 | 1056 | 3.0237 |
| B | 23 | 3.75 | 990 | 2.9956 |
| A | 21 | 3.333 | 880 | 2.9445 |
| G | 19 | 3 | 792 | 2.8987 |
| F | 17 | 2.667 | 704 | 2.8476 |
| E | 16 | 2.5 | 660 | 2.8195 |
| D | 14 | 2.25 | 594 | 2.7738 |
| C'' | 12 | 2 | 528 | 2.7226 |
| B | 11 | 1.875 | 495 | 2.6946 |
| A | 9 | 1.667 | 440 | 2.6435 |
| G | 7 | 1.5 | 396 | 2.5977 |
| F | 5 | 1.333 | 352 | 2.5465 |
| E | 4 | 1.25 | 330 | 2.5185 |
| D | 2 | 1.125 | 297 | 2.4728 |
| C' | 0 | 1 | 264 | 2.4216 |
The frequency difference between C' and C'' is 264 Hz; betwen C'' and C''' it is 528Hz, twice as large. One octave is not a fixed frequency difference but a frequency ratio of 2:1. The size of each semitone in Hz gets larger as we go higher up the musical scale (figure 1). If we could squash the frequency scale so that higher semitones are the same size as lower semitones we would be using a logarithmic scale (figure 2). On the logarithmic frequency scale, the difference between C' and C'' is the same as the difference between C'' and C'''.
Amplitude and loudness
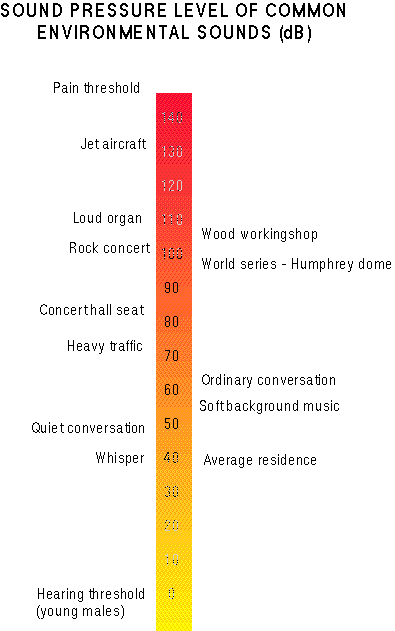
The perception of loudness is also more nearly logarithmic than linear. In honour of Alexander Graham Bell, the inventor of the telephone, the term bel was given to a unit on the logarithmic scale of acoustical power (intensity) ratio. The interval between the measured intensity W 1 and the baseline (reference) intensity W0 in bels is log10 (W1 / W0). 1 bel is a ratio of 10:1, 2 bel a ratio of 100:1. This unit is too large for practical purposes, so the decibel (dB), one-tenth of a bel, is more commonly used. 1 dB (intensity level, or IL) = 10 log10 (W1 / W0). In speech acoustics, the reference intensity W0 is usually the threshold of hearing, 10-10 W/m2, which corresponds to a sound pressure P0 of 20 µPa (20 millionths of a Pascal, or 0.00002 Pa). Since intensity is proportional to the square of sound pressure, a decibel is 20 times the logarithm of the measured pressure divided by the reference pressure: 1 dB (sound pressure level, or SPL) = 20 log10 (P1 / P0).
