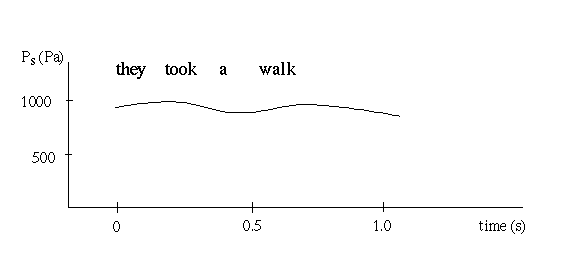
Fig. 1. Typical record of Ps versus time during a sentence. Sometimes there is a slight fall in Ps towards the end of a sentence, as the loudness falls.
1. Modulation of air
Speech is produced by modulating the flow of air from the lungs. The modulation always occurs by making a narrow constriction in the airways. The constriction may be at the larynx, or in the supraglottal tract, or both.
There are two principal types of modulation: quasiperiodic modulation through vocal cord vibration, and random modulation of the air stream due to turbulence in the flow. This modulation produces sound sources in the vocal tract. These sources form the excitation for the acoustic resonator formed by the vocal tract, and the sound that is generated by the sources is modified or filtered by the resonator. The sound that results is radiated from the mouth and/or nose.
We shall examine (1) the properties of the sources and (2) the acoustic
characteristics of tubes or resonators of various sizes and shapes.
2. Pressure and air flow during speech production
The pressure below the glottis (subglottal pressure) Ps is typically in the range of 600-1200 Pa during speech production. The flow of air during speech production can range from zero (during a stop consonant) up to 1000 cm3/s (0.001 m3/s) or more (during an [h] or an aspirated stop). The pressure in the lungs and the pressure just below the glottis are usually about the same during speech production. In normal breathing (not speech), the subglottal pressure may be 100 Pa or less.
During the production of a sentence the subglottal pressure normally
remains fairly constant. We do not exert rapid control over Ps from
one speech sound to the next. There are momentary greaterthannormal
decreases in lung volume during emphatically stressed syllables (Ohala
1990), which may lead to momentary increases in Ps.

Fig. 1. Typical record of Ps versus
time during a sentence. Sometimes there is a slight fall in Ps
towards the end of a sentence, as the loudness falls.
3. Some concepts and relations concerning pressure, air flow, and volume
When we talk about pressure in the context of speech production, we usually mean the amount of pressure above or below atmospheric pressure. A typical pressure in the lungs (and immediately below the glottis) during speech production is 1000 Pa above atmospheric pressure. It may be larger than this when we speak loudly, and smaller than this when we speak softly.
Some authors measure pressure in cm H2O. 1 cm H2O = c. 100 Pa (98 Pa, more accurately). Atmospheric pressure is about 100,000 Pa (101 325 Pa, more exactly). Thus the pressure in the lungs when we speak is about 1% above atmospheric pressure.
3.1. How pressure changes when we change the shape of the closed vocal tract
If we take a closed volume V1, in which the total pressure (including atmospheric pressure) is P1, and we change the volume to V2, there will be a change in pressure to P2 such that P1 V1 = P2 V2.
Example 1. Suppose we close off the lips, glottis and velopharyngeal opening of the vocal tract, such that the oral volume is, say, 70 cm3 (0.00007 m3). With all these openings sealed, we now raise the larynx (as we do to produce an ejective consonant) such that the total volume is reduced by 2 cm3 (0.000002 m3), to become 68 cm3. Suppose the initial pressure P1 in the mouth was atmospheric pressure. What is the pressure P2 in the mouth after the larynx is raised?
P1 V1 = P2 V2
101325 × 0.00007 = P2 × 0.000068
P2 = (0.00007 ÷ 0.000068) × 101325 = 104305 Pa, or about 3000 Pa above atmospheric pressure.
Exercise 1. Suppose that during the production of an implosive the larynx is lowered, so that the total volume in the mouth is increased by 1.5 cm3. What is the resulting pressure P2 in the mouth?
Example 2. Suppose again that the vocal tract volume V is 70 cm3 and is closed off at the lips and velopharyngeal opening. Due to vocal cord vibration some additional volume of air is introduced into the vocal tract until the pressure in the mouth becomes 1000 Pa above atmospheric pressure. By what additional volume DV would the vocal tract have to be reduced to bring about this degree of pressure increase? Let P = atmospheric pressure, DP = 1000 Pa.
P2V2 = (P1 + DP) (V1 + DV)
~ P1V1 + V1 DP + P1 DV
i.e. DV = - V1 DP ÷ P1
= - 0.00007 × 1000 ÷ 101325
= -0.0000007 m3, or - 0.7 cm3
(The sign is negative, because you would have to reduce the volume of air to bring about an equivalent degree of pressure increase. ) Thus changing volume by 0.7 cm3 causes a change in pressure of 1000 Pa.
When we take a breath during normal breathing or during speech production, we usually take about 1 to 2 litres of air (0.001 - 0.002 m3). On the average, the rate of air flow during speech production may be about 0.0002 m3/s (200 cm3/s), but at any moment in time there may be large fluctuations about this average value.
4. Air flow and pressure drop at a constriction
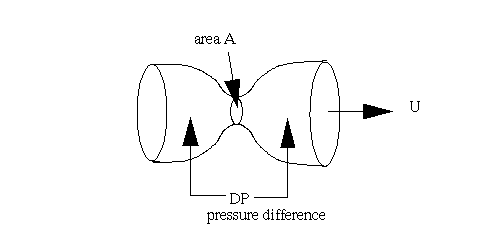
DP = pressure drop (Pa)
U = volume velocity of the airflow (m3/s)
r = density (kg/m3), about 1.225 kg/m3 for air
DP = K1 U + K2 r U2/2A2
Term 1 : K1 U. The pressure drop is proportional to air flow. K1 depends on the dimensions of the constriction: K1 is large when the constriction size is small. This term in the equation predominates when A is small (A < 0.01 cm2?), in which case term 2 might as well be ignored.
Term 2 : K2 r U2/2A2. The pressure drop is proportional to U2. The constant K2 is about 0.9 (±20%, depending on the constriction shape and location). This term depends only on the crosssectional area of the constriction, and not its length or width. This term is usually much larger than term 1.
There may be a pressure drop at the glottis, or at a supraglottal constriction,
or both.
5. Ways of controlling air pressures and flows
There are a number of ways we can control air pressures and air flows
during speech. We can raise or lower the subglottal pressure, but Ps
does not usually change much during a sentence. We can manipulate the opening
at the larynx; we can manipulate the supraglottal constriction; we can
manipulate the velopharyngeal opening; we can manipulate the supraglottal
volume either by raising or lowering the larynx or by expanding or contracting
the vocaltract walls. We can make sounds by producing only one constriction
(e.g. vowels), or two constrictions (e.g. fricatives and stops), or sometimes
three constrictions (e.g. clicks).
6. Some typical constriction sizes, air flow rates, etc.
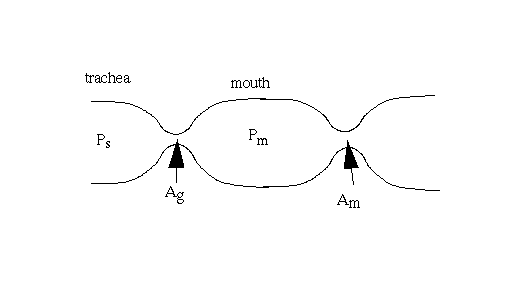 |
||||
| Vowels | Areas | Vocal cords vibrating
Ag ~ 0.1-0.2 cm2 |
0.3 cm2 < Am < 3 cm2 | |
| Flow | Ug= about 150 cm3/s | |||
| Pressures | Ps ~ 500-800 Pa | Pm ~ 0 | ||
| [h], aspiration | Areas | Ag ~ 0.3 cm2 | Am > 0.3 cm2 | |
| Flow | about 1000 cm3/s (1 litre/s) | |||
| Pm | 0 | |||
| glottal stop | Areas | Ag = 0 | Am > 0.3 cm2 | |
| Flow | 0 | |||
| Pm | 0 | |||
| fricatives | Areas | Ag ~ 0.1-0.2 cm2 | Am ~ 0.1 cm2 | |
| Flow | Ug= about 300 cm3/s | |||
| Pm | 300-800 Pa | |||
| prevoicing in [b, d, g] | Areas | Vocal cords vibrating
Ag ~ 0.1-0.2 cm2(maximum) |
Am = 0 | |
| Flows | about 100 cm3/s | Um = 0 | ||
| Pm | about 600 Pa | |||
| voiceless stops | Areas | Ag ~ 0.1-0.3 cm2 | Am = 0 | |
| Flows | Ug= 0 | Um = 0 | ||
| Pm | about 1000 Pa (Pm = Ps) | |||
Acknowledgement
These course notes are based on unpublished lecture notes entitled ``physiological and acoustic phonetics'', by Prof. Ken Stevens (MIT), presented at the Linguistics Institution, University of Stockholm.
References
Ohala, J. J. (1990) Respiratory activity in speech. In W. J. Hardcastle and A. Marchal, eds. Speech Production and Speech Modelling. Dordrecht: Kluwer. 23-53.
See also Stevens, K. N. (1998) Acoustic Phonetics. Cambridge, MA: The MIT Press. Chapter 1,