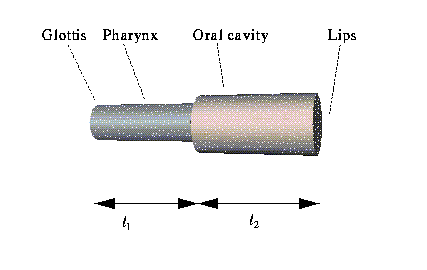
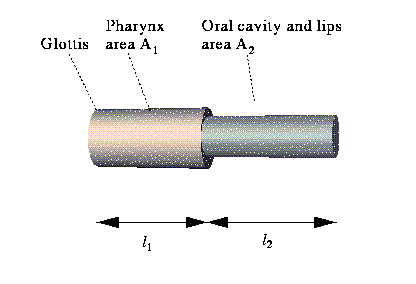
We examine the disturbance of volume-velocity amplitude in the tube, associated with a particular natural frequency or formant.

1. Reduction in cross-sectional area of the tube at a place where the volume velocity amplitude is a maximum causes a lowering of that fomant frequency.
2. Reduction in cross-sectional area at a place where the volume velocity amplitude is a minimum causes a raising of that formant frequency.
3. Increasing the cross-sectional area at the places indicated in (1) and (2) above causes the opposite effect on the formant frequency.

2.1. Altering F₁
 

Perturbation to rear half of tube:	Perturbation to front half of tube:		Effect on F1
Narrowing	Enlargement		F1 increases
Enlargement	Narrowing		F1 decreases

2.2. Altering F₂

Dividing the tube into six sections of equal length (say, 2.83 cm):

Section 1		Sections 2 and 3		Sections 4 and 5		Section 6		Effect on F2
Narrowing		Enlargement		Narrowing		Enlargement		F2 increases

2.3. Altering F₃

Dividing the tube into ten equal sections (of e.g. 1.7 cm):

Section 1

Sections 2 and 3

Sections 4 and 5

Sections 6 and 7

Sections 8 and 9

Section 10

Effect on F3

Narrowing

Enlargement

Narrowing

Enlargement

Narrowing

Englargement

F3 increases

3. Some simple approximations to vocal-tract shapes for vowels

Some vocal tract shapes can be approximated by connecting together two or more uniform tubes with different cross-sectional areas. Under some conditions, the formant frequencies for this combination of tubes can be calculated from simple formulas.

3.1. First, we note the natural frequencies of uniform tubes with different opened or closed conditions at the ends.

For a tube of length l, closed at one end, f = c/4l, 3c/4l, 5c/4l, ..., where c is the velocity of sound in air.

For a tube open at both ends, f = c/2l, c/l, 3c/2l, ...

For a tube closed at both ends, f = c/2l, c/l, 3c/2l, ...

Also, the formula for the lowest natural frequency for a tube with a narrow opening at one end:

 

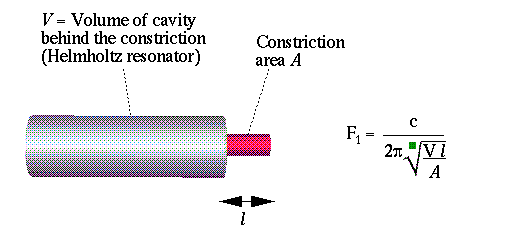
3.2. Approximation to the vowel []:

Vocal tract profile of natural (Japanese) []:

This configuration can be modelled as a combination of two tubes closed at one end, one of length l₁, the other of length l₂. If the pharynx tube is small compared with the front tube, then the natural frequencies of the combination of two tubes (at left) are the natural frequencies of the individual component tubes, i.e., c/4l₁, 3c/4l₁, ..., c/4l₂, 3c/4l₂, ...

Typical values (for an adult male vocal tract) are l₁ = 8 cm, l₁ = 9 cm, so we have resonances at 1063, 3188, ... Hz for the rear tube and 944, 2833, ... Hz for the front tube. Or, arranging the frequencies in order,

F₁ = 944 Hz, F₂ = 1063 Hz, F₃ = 2833 Hz, etc.

Note that F₁ is greater than 500 Hz and F₂ is less than 1500 Hz, as predicted by the method of section 2.
 

3.3. Approximation for vowel [i]:

Vocal tract profile of (Japanese) [i]:

In this case, the resonances of the rear tube are those of a tube closed at both ends, and the resonances of the front tube are those of a tube open at both ends. Again, the natural frequencies of the combination of two tubes (at left) are the natural frequencies of the individual components (at right), except that we must also include the Helmholz resonant frequency since we have a volume V= l₁A₁ terminated by a narrow tube. Thus we have:

Typical values are l₁ = 9 cm, l₂ = 8 cm, A₁ = 5 cm², A₂ = 0.5 cm². Thus F₁ = 202 Hz, F₂ = 1890 Hz, F₃ = 2125 Hz, etc. (These are approximations only to the formant frequencies for [i].)

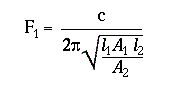
3.5. Uniform vocal-tract shape with lip-rounding (a very rough approximation for vowel [u] - more like [], in fact).

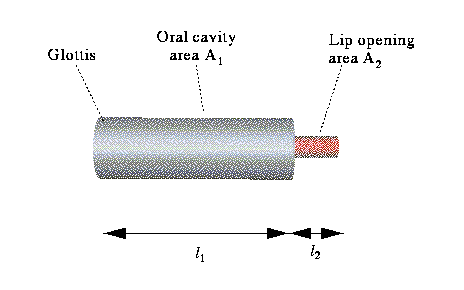
This tube has the same geometry and resonance conditions as the previous example, but the dimensions are different. Roughly, we have l₁ = 15 cm, A₁ = 5 cm², l₂ = 2 cm, A₂ = 0.3 cm²,

Thus, F₁ = 242 Hz.

The second formant is approximately the lowest resonance of the larger tube, closed at both ends, which is F2 = c/2l₂ = 1133 Hz.

4. Vowel spectra: relations between formant amplitudes and formant frequencies

The formant frequencies for vowels are represented as peaks in the spectra of the vowels. However, as the frequencies of the formants change from one vowel to another, their relative amplitudes also change.

These changes in the amplitudes of the formants can be predicted from theoretical considerations, and are in accordance with the following rules:

1. If a particular formant shifts downwards in frequency, the amplitudes of the higher frequency formants decrease; if the formant shifts upwards in frequency, then the amplitudes of the higher frequency formants increase.
2. If two formants come close together in frequency, the amplitudes of both are increased.
3. When a formant shifts downwards in frequency, the amplitude of that formant decreases. Likewise, if a formant shifts upwards in frequency, its amplitude increases. This rule is particularly important for the first formant: a downward shift of the frequency of the first formant results in a decrease in the amplitude of the first formant, and consequently a decrease in the amplitude of the vowel (since the overall amplitude of the vowel is determined primarily by the amplitude of the first formant).