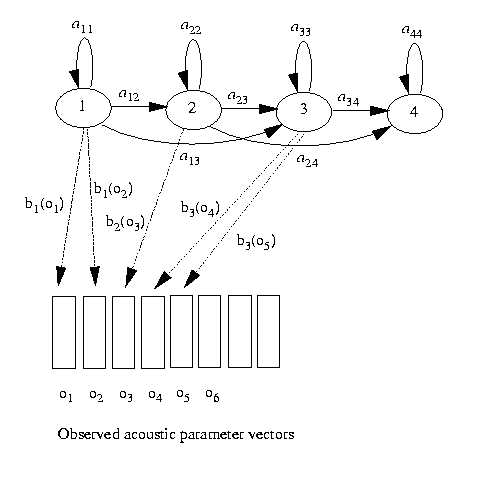
Figure 7.6. An HMM for generating acoustic parameter vectors
The examples discussed so far illustrate the general characteristics
of an HMM. Now, instead of generating strings of just two symbols (H and
T), consider a model that generates acoustic parameter vectors.
To make the explanation simpler, assume that the acoustic parameter
vectors
are represented as codebook numbers. That is, the alphabet of the model
output is a (smallish) set of numbers, instead of H and T.
Figure 7.6. An HMM for generating acoustic parameter vectors

There is one acoustic vector per frame (e.g. each 10 ms interval of a signal), and transitions between states correspond to transitions from one frame to the next. If the acoustic vector does not change from one frame to the next, it is possible to remain in a state. Also, if the acoustic vector does change, it is still possible to remain in a state. But it is also possible, under either condition, to change state.
In the coing-tossing models and in the weather model, state transitions were permitted from each state to every other state. Such fully-connected models are called ergodic. When each state transitions corresponds to a change from one frame to the next, we are constrained by the laws of time as to which transitions are possible. The model in figure 7.6 exemplifies the subset of HMMs called "left-to-right" or Bakis models.