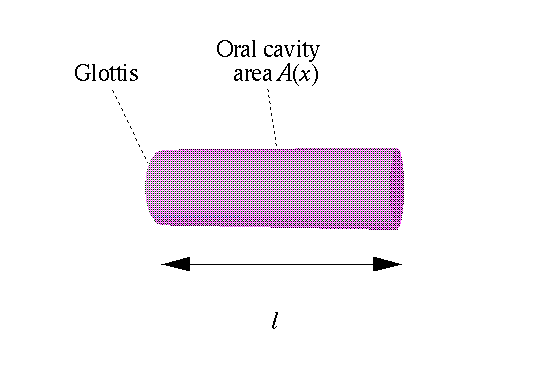
Tube is open at one end, closed at the other. From physics, it can be shown that this tube has a number of natural frequencies, given by
1. Formant frequencies of a uniform tube (A(x) = constant)
Tube is open at one end, closed at the other. From physics, it can
be shown that this tube has a number of natural frequencies, given by
f = c/4l, 3c/4l, 5c/4l, ...
where c = velocity of sound, c. 340 m/s. (We assume that the cross-sectional
dimensions of the tube (e.g. its diameter) are much smaller than the length
l.)
Note that c = f
, where
= wavelength. The lowest formant frequency c/4l occurs, therefore,
when = 4l, i.e., the
tube is ¼ wavelength.
The cross-sectional area of the vocal tract is, in fact, almost uniform
for the schwa vowel [
]. For a typical
adult male, the length of the vocal tract is l = 0.17 m, approximately.
Thus for a vowel produced with uniform cross-sectional area, we have
F1 = c/4l = 340/4 × 0.17 = 500 Hz.
F2 = 1500 Hz
F3 = 2500 Hz
etc.
The spectrum of the vowel [],
then, is like the following figure (which shows the measured spectrum of
the word "err", spoken by a male speaker):
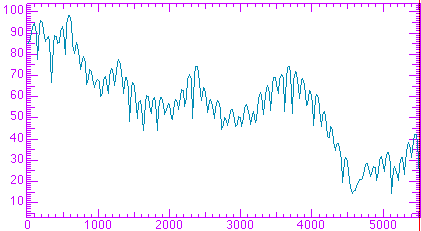
The bandwidths of the formants (widths of formant peaks measured at a height that is 70% of the height of the peak) are roughly 50 Hz for the first formant, 50 - 80 Hz for the second formant, and 80 - 150 Hz for the third formant. The first formant peak always has the largest amplitude of all the formants.
The formants are all shifted upward if the length l of the vocal
tract is shortened. An average length for an adult female vocal tract is
0.15 m, in which case, for the vowel [],
the calculated formant frequencies are 567, 1700, 2833, 3967 Hz, etc. A
real example, showing the spectrum of the word "err" spoken by a female
speaker, looks like this:
The formants are also shifted upwards in frequency if the vocal tract is filled with a gas (such as a mixture of helium and oxygen) for which the velocity of sound c is greater than that for air.
For a given vocal-tract shape, changing the fundamental frequency (f0) does not change the positions of the formant peaks in the spectrum. The harmonics just move up or down under a fixed spectrum envelope when f0 is increased or decreased.